poplaze.blogg.se - Allmänt

DATA ERROR CYCLIC REDUNDANCY CHECK RAW GENERATOR
DATA ERROR CYCLIC REDUNDANCY CHECK RAW CODE

Otherwise, the data is assumed to be error-free (though, with some small probability, it may contain undetected errors this is inherent in the nature of error-checking). The device may take corrective action, such as rereading the block or requesting that it be sent again. If the CRC values do not match, then the block contains a data error. When a codeword is received or read, the device either compares its check value with one freshly calculated from the data block, or equivalently, performs a CRC on the whole codeword and compares the resulting check value with an expected residue constant.

DATA ERROR CYCLIC REDUNDANCY CHECK RAW GENERATOR

The simplest error-detection system, the parity bit, is in fact a 1-bit CRC: it uses the generator polynomial x + 1 (two terms), and has the name CRC-1.Ī CRC-enabled device calculates a short, fixed-length binary sequence, known as the check value or CRC, for each block of data to be sent or stored and appends it to the data, forming a codeword. The CRC and associated polynomial typically have a name of the form CRC- n-XXX as in the table below. Note that most polynomial specifications either drop the MSB or LSB, since they are always 1. In other words, the polynomial has a length of n + 1 its encoding requires n + 1 bits. Such a polynomial has highest degree n, which means it has n + 1 terms. For a given n, multiple CRCs are possible, each with a different polynomial. The two elements are usually called 0 and 1, comfortably matching computer architecture.Ī CRC is called an n-bit CRC when its check value is n bits long. In practice, all commonly used CRCs employ the Galois field, or more simply a finite field, of two elements, GF(2). The important caveat is that the polynomial coefficients are calculated according to the arithmetic of a finite field, so the addition operation can always be performed bitwise-parallel (there is no carry between digits). This polynomial becomes the divisor in a polynomial long division, which takes the message as the dividend and in which the quotient is discarded and the remainder becomes the result.

DATA ERROR CYCLIC REDUNDANCY CHECK RAW CODE

Specification of a CRC code requires definition of a so-called generator polynomial.

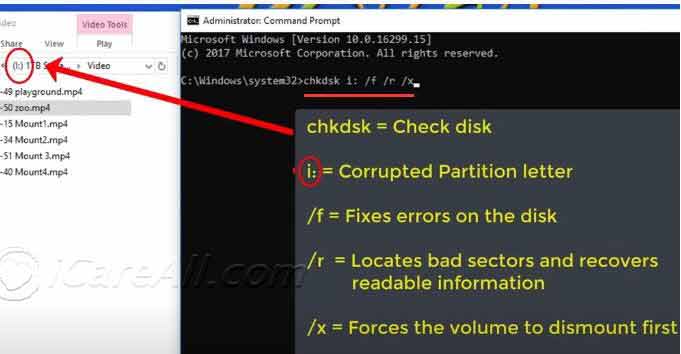
Typically an n-bit CRC applied to a data block of arbitrary length will detect any single error burst not longer than n bits, and the fraction of all longer error bursts that it will detect is (1 − 2 − n). This is important because burst errors are common transmission errors in many communication channels, including magnetic and optical storage devices. Ĭyclic codes are not only simple to implement but have the benefit of being particularly well suited for the detection of burst errors: contiguous sequences of erroneous data symbols in messages. The use of systematic cyclic codes, which encode messages by adding a fixed-length check value, for the purpose of error detection in communication networks, was first proposed by W.

9 Polynomial representations of cyclic redundancy checksĬRCs are based on the theory of cyclic error-correcting codes.

Because the check value has a fixed length, the function that generates it is occasionally used as a hash function. CRCs are popular because they are simple to implement in binary hardware, easy to analyze mathematically, and particularly good at detecting common errors caused by noise in transmission channels. ĬRCs are so called because the check (data verification) value is a redundancy (it expands the message without adding information) and the algorithm is based on cyclic codes. CRCs can be used for error correction (see bitfilters). On retrieval, the calculation is repeated and, in the event the check values do not match, corrective action can be taken against data corruption. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents.

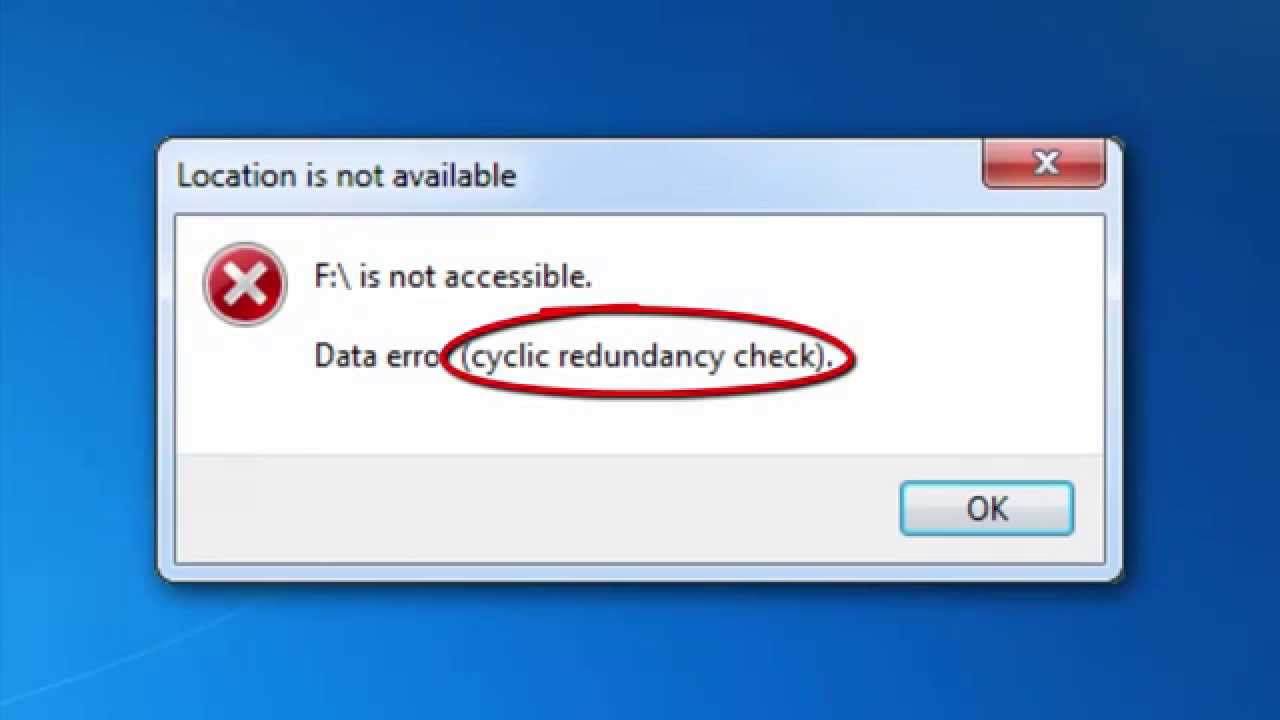
Error-detecting code for detecting data changesĪ cyclic redundancy check ( CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to raw data.